Hoy traemos un post más volcado a la tecnología del Bitcoin. Vamos a ver exactamente que es la clave privada y como determinar la clave pública correspondiente, base fundamental de gran parte de la seguridad del Bitcoin!
Firmas digitales
Como veíamos en el post sobre billeteras, nuestra clave privada es lo que nos permite demostrar la propiedad de nuestros Bitcoin, indispensable a la hora de realizar transacciones. Al enviar Bitcoin de una Billetera a otra una de las cosas que debemos hacer es firmar digitalmente la transacción, para ello usamos la clave privada.
El concepto de firma digital es equivalente al de la firma física la cual confiere autenticidad al documento/archivo/mensaje firmado.
Veamos la clásica comparación entre firma digital y la firma física de un cheque. Cuando firmamos un cheque estamos dando prueba que hemos sido nosotros quienes autorizamos la transacción. En caso de que otra persona quiera firmar un cheque nuestro, falsificando la firma, el mismo no será aceptado. En el mismo sentido la firma digital prueba que el mensaje fue firmado por alguien con conocimiento de la clave privada!
La red de Bitcoin valida luego la transacción teniendo los datos de la misma, la firma digital correspondiente, y nuestra clave pública. No se precisa la clave privada para validar transacciones, se validan con la clave pública y ésta no da permisos para hacer modificaciones ni generar nuevas transacciones.
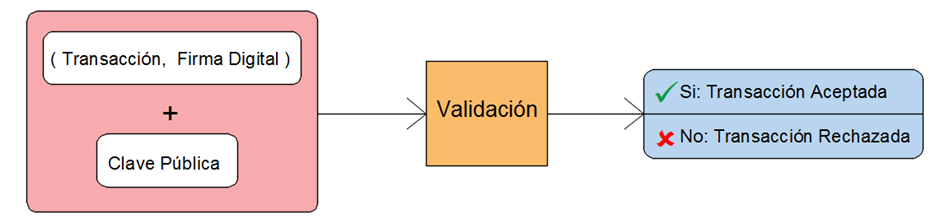
En siguientes posts veremos cómo se hace para validar las transacciones!
El algoritmo criptográfico usado para firmar transacciones en Bitcoin es el llamado Algoritmo de Firma Digital de Curva Elíptica, ECDSA por sus siglas en inglés (Elliptic Curve Digital Signature Algorithm).
Por ahora no entraremos en más detalles sobre el funcionamiento del ECDSA, haremos una parada intermedia sobre cómo se generan las claves. Varios de los fundamentos que usaremos en el camino servirán luego para explicar el ECDSA.
¿Cómo se generan las claves privadas y públicas?
Recordarán que como decíamos en posts anteriores la clave privada es un número aleatorio entre 1 y otro número extremadamente grande. Tan grande que no resulta practico ni viable intentar descubrir la clave privada asociada a una dirección de Bitcoin. Este número es levemente inferior a 2256 , un número con 77 cifras!!
Es un número tan grande que hay más claves privadas posibles que granos de arena en el mundo, muchas, muchas más. Ya haremos algún post estudiando que tan grande es 2256!
El número de posibles claves privadas es exactamente: n-1= 115792089237316195423570985008687907852837564279074904382605163141518161494336
Más adelante veremos porque lo llamamos n-1 y quien es n!
Usualmente no es necesario elegir directamente la clave privada si no que una aplicación como una billetera lo hace por nosotros. Un ejemplo es la paper wallet del siguiente link, donde a partir del movimiento del mouse se genera la clave privada de forma pseudoaleatoria.
https://bitcoinpaperwallet.com/bitcoinpaperwallet/generate-wallet.html
Curvas Elípticas
¿Cómo se determina la clave pública a partir de la clave privada? La clave pública es el resultado de realizar operaciones matemáticas sobre la clave privada.
La clave pública está formada por dos números que representan un punto P sobre una curva E. El punto P queda definido por sus coordenadas x e y que deben pertenecer a la curva E, P=(xp,yp).
Las curvas elípticas son todas las curvas de la forma:
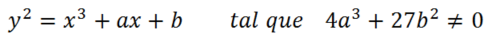
En otras palabras, decimos que los puntos (x,y) pertenecen a la curva si la coordenada del eje “y” (eje vertical) elevado al cuadrado (y2) es igual a la coordenada “x” (eje horizontal) elevado a la 3 más el número 7 (x3+7). Si unimos los puntos (x,y) con que cumplen este criterio obtenemos una línea curva, la llamada curva elíptica.
La condición que deben cumplir los términos a y b es necesaria para evitar algunos casos particulares que darían lugar a problemas.
En el caso de Bitcoin a=0 y b=7, es decir la ecuación que define nuestra curva E es:
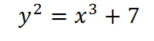
A continuación el grafico de nuestra curva, graficada hasta x=6.
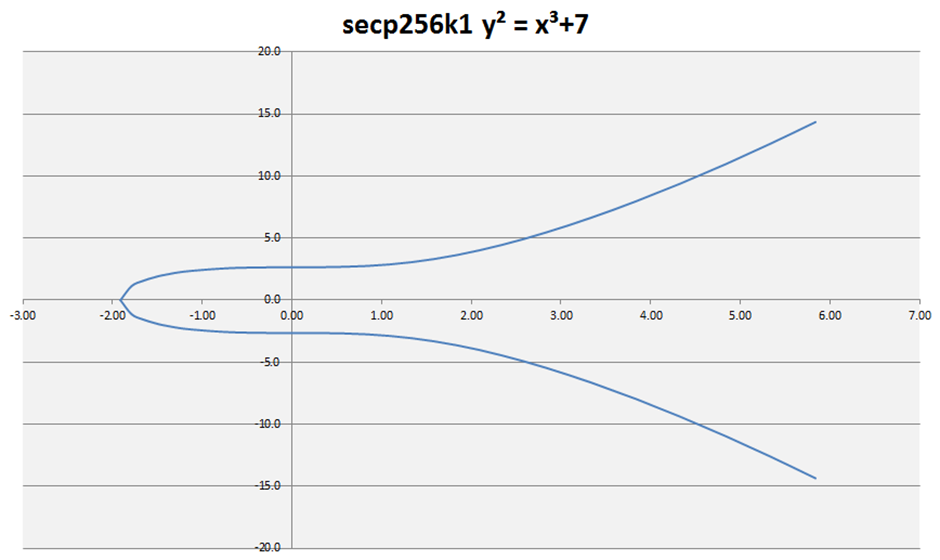
Como se puede ver, la curva es simétrica respecto del eje x, es decir que para todo punto P=(xp,yp) que pertenece a la curva, el punto de coordenadas P’=(xp,-yp) también pertenece a la curva.
Algunas veces se le llama –P a P’=(xp,-yp). Para no confundir el signo “-“ antes del punto P, con el signo “-“ antes de un número entero que significa el valor negativo, preferimos seguir usando P’ para el punto de coordenadas (xp,-yp) .
La clave pública es el resultado de multiplicar la clave privada por un punto G de la curva, que llamamos Generador.
Es decir, si designamos nuestra clave privada como kpr entonces nuestra clave pública kpu, es kpu = kpr * G. Notar que kpr es un numero entero y G un punto en la curva. Usamos la letra k para las claves por su nombre en inglés Key (Clave).
En el caso de Bitcoin, G es el punto de coordenadas (xG, yG) donde:
xG=55066263022277343669578718895168534326250603453777594175500187360389116729240
yG=32670510020758816978083085130507043184471273380659243275938904335757337482424
¿Cómo es eso de multiplicar un punto en una curva?
Recordemos que multiplicar un numero x por otro número n no es más que sumar x n veces.
Es decir:
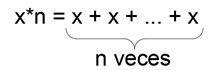
Precisamos entonces definir la operación suma de puntos en una curva, para poder multiplicar kpr por G.
La suma de puntos P(xp,yp) y Q(xq,yq) sobre la curva elíptica se define como el punto en la curva tal que es el simétrico respecto del eje x del punto de intersección entre nuestra curva y la recta r que une P con Q.
Es decir, para encontrar P+Q seguimos los siguientes pasos:
- Trazamos la recta r que une P con Q
- El punto en que la recta r corta a nuestra curva E lo llamamos (P+Q)’. (P+Q)’ = (xp+q ,yp+q)
- Buscamos el punto simétrico respecto del eje x, es decir aquel con igual coordenada x que (P+Q)’ pero opuesto signo en la coordenada “y”. Este es nuestro punto P+Q = (xp+q ,-yp+q)
En la imagen a continuación se muestra el procedimiento gráficamente.
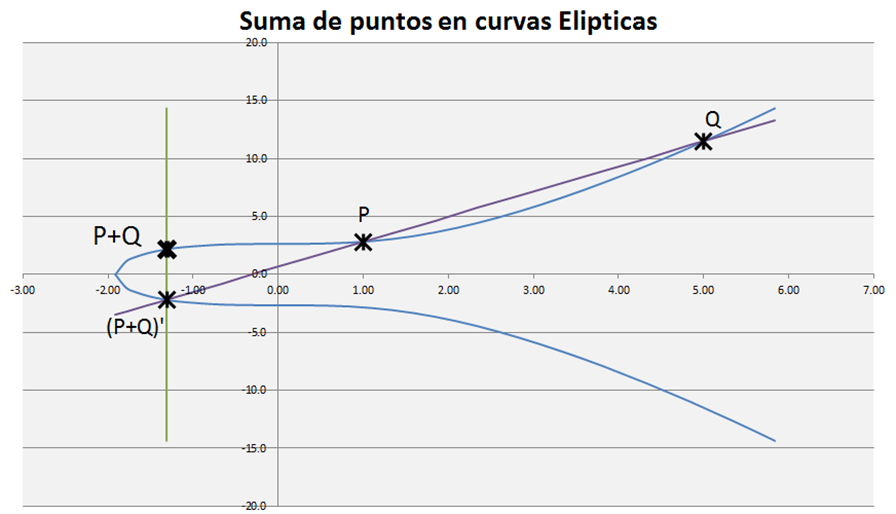
Las ecuaciones que determinan analíticamente la coordenada xp+q y yp+q son
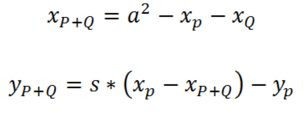
Donde s, la pendiente de la recta r, es:
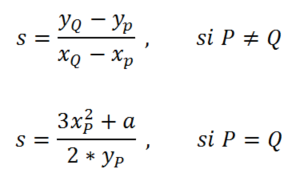
Al igual que con los números entero, para multiplicar puntos en la curva lo que hacemos es sumar un punto a si mismo n veces.
¿Cómo definimos entonces la suma de un mismo punto, es decir como calculamos P+P? Para ello seguimos los mismos pasos que para hacer P+Q salvo que la recta r no es más que la tangente a la curva en el punto P.
Esto resulta intuitivo dado que si vamos moviendo el punto Q por la curva hasta llegar al punto P la recta r se transforma en la tangente a la curva en el punto P y su pendiente es la dada en las formulas anteriores para P=Q.
Dejamos el siguiente link con una planilla de Excel para experimentar! Probar a mover Q hacia P para ver como la recta queda tangente en P!
Con esto ya casi podemos calcular nuestra clave pública en función de nuestra clave privada!
Un poco más de matemáticas y estamos!
La seguridad de los algoritmos criptográficos basados en curvas elípticas, y de otros tipos, está dada por el problema del logaritmo discreto en cuerpos finitos….”que no panda el cúnico” que es más sencillo de lo que suena! Bueno en realidad no es tan sencillo pero lo vamos a simplificar un poco!
Por ahora nos centramos en que precisamos un conjunto finito de números (opuesto de infinito). Por ejemplo, podemos tomar los enteros positivos menores a 19, es decir {0,1,2,3,…,19}.
Vamos a precisar sumar los elementos de nuestro conjunto, pero ¿cómo hacer para poder sumar elementos de nuestro conjunto de números y no salirnos de él?
Por ejemplo, si tomamos los enteros menores a 19, ¿cómo hacemos para poder sumar 17+17 y que sea un número menor a 19? Empieza a aparecer la magia de la matemática!
Para ello usamos la operación módulo!
La operación módulo es como sumar horas en un reloj. Supongamos que tenemos un reloj de 12 horas. Si son las 10 horas y pasan +7 horas más estamos en la hora 5, es decir la hora 17 es “igual” a la hora 5.
Escribimos entonces que 17 = 5 mod 12, es decir, 17 es igual a 5 módulo 12.
Cuando decimos que a=r mod p estamos diciendo que a es el resto de dividir r entre p.
Cada vez que pasamos por 12 empezamos a contar desde 0 de nuevo. Esta es una definición totalmente informal pero útil conceptualmente.
De esta forma 12 mod 12 = 0, nuestro conjunto es el formado por el 0 y los demás números enteros menores a 12, es decir del 0 al 11, lo representamos como: {0,1,2,…,11}. Generalizando, si trabajamos en modulo p, el mayor valor del conjunto es p-1.
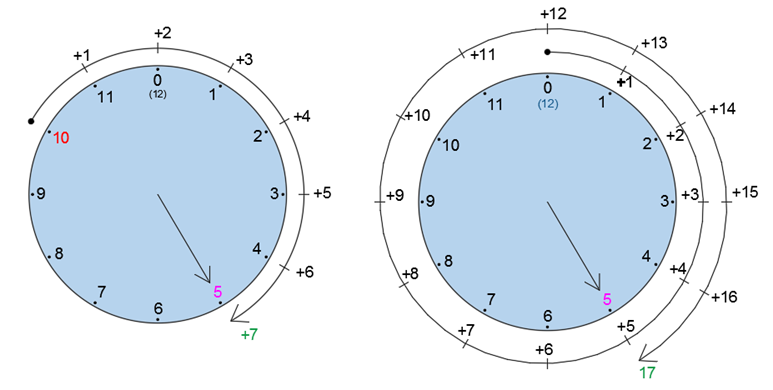
Podemos notar que también 17+12 = 29 = 5 mod 12, y que 5 es la cantidad de unidades que nos pasamos del 12 al dar dos vueltas. Veamos, dos vueltas son 12+12=24, y con 5 más llegamos a 29, por lo que 29 = 5 mod 12, ya que nos pasamos por 5 luego de la segunda vuelta por las 12.
Si en vez de operar en módulo 12 operamos en modulo p entonces basta con pasar a un “reloj” de p horas!
Utilizaremos un valor particular de p, que además de ser un número muy grande es un número primo.
Recordar que un número es primo si únicamente se puede dividir por sí mismo o por 1. Por ejemplo, el numero 6 no es primo ya que 3*2=6, pero el 7 si, ya que 7 dividido cualquier otro número entero menor que él, da como resultado un número con coma, es decir no es entero.
El número primo que se usa en Bitcoin es p=2256-232-29-28-27-26-24-1 = 115792089237316195423570985008687907853269984665640564039457584007908834671663
Lo que hacemos entonces en el caso de Bitcoin es tomar las mismas ecuaciones de la curva elliptica pero mod p.
¿Por qué usamos esta curva y no otra? y ¿por qué usamos este valor de p y G?
Esta curva junto con este valor de p y G se llama secp256k1 y fue desarrollada o propuesta por el grupo SECG, un consorcio fundado por Certicom en 1998 con el objetivo de desarrollar estándares comerciales para el uso eficiente de criptografía basada en ECC (criptografía de curva elíptica por sus siglas en ingles).
Se puede encontrar la publicación original en el siguiente link.
https://www.secg.org/sec2-v2.pdf
La razón por la cual Satoshi Nakamoto, creador de Bitcoin, eligió esta curva y no otra no lo sabremos exactamente pero se cree que es dado a que se sospecha que es una de las más seguras y por ser computacionalmente eficiente.
¿Que implica tomar las ecuaciones mod p?
En primer lugar x e y deben pertenecer al conjunto {0,…,p-1} donde p es el ya definido 2256-232-29-28-27-26-24-1. Notar que de esta forma la gráfica ya no es más una curva y pasa a ser un conjunto de puntos aislados.
Luego realizamos las operaciones de cada lado del signo de igual que definen la curva elíptica y aplicamos la función módulo.
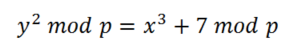
Grafiquemos esto para ver cómo se ve! Si usamos el valor de p de la curva secp256k1 tendríamos muchísimos valores de x e y para considerar. Tomemos p=23 por un segundo para ver cómo quedaría la curva.

Tomemos x=4 y encontremos el valor y que satisface la ecuación de la curva elíptica mod 23.
Sustituimos el 4 en la ecuación anterior: x3+7= 43+7=71.
Ahora calculamos 71 en módulo 23 utilizando la definición del resto de la división: Vemos que 71/23=3.086…., si restamos 71-3*23 obtenemos que el resto es 2, es decir 2=71 mod 23.
Precisamos ahora encontrar un valor de y tal que y² mod 23 = 2, es decir que y² se pase de 2 en un reloj de 23 horas. Por ejemplo nos sirve y²=25, vemos que 52=25 por lo que y=5 es una solución, encontramos así que el punto (4,5) pertenece a nuestra curva elíptica mod 23!!
Notar que de no tomar el módulo 23 de ambos lado la ecuación no se cumple ya que quedaría 25=71 lo cual es falso! Es decir que el punto (4,5) no pertenece a la curva sin aplicar mod p de ambos lados. Por lo tanto, la curva mod p “no tiene nada que ver” con la curva sin mod p.
¿Cómo hacemos ahora para sumar puntos? Simplemente usamos las mismas ecuaciones que antes pero aplicando mod p, es deci
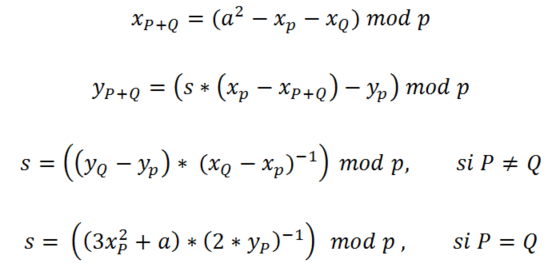
Notar que hemos cambiado la división por multiplicar por el inverso en las ecuaciones de la pendiente, lo cual es “equivalente”. Hacemos esto simplemente para mantener un poco la formalidad matemática.
El inverso de un número a de nuestro conjunto bajo modulo p es otro valor b tal que
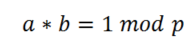
Se escribe
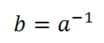
Es decir:
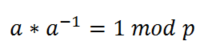
Notar que el -1 es una notación, no una operación.
A diferencia de lo que sucede con los números reales no todo número tiene un inverso al trabajar en aritmética modular.
Un número a tiene inverso modulo p si y solo si el máximo común divisor entre a y p es 1. Es decir a tiene un inverso modulo p si y sólo si se cumple que el mcd(a,p)=1. El máximo común divisor entre dos número es el mayor entero que los divide a ambos con resto 0, se dice que a y p son coprimos.
Ejemplo: El mcd(15,35) = 5 ya que 15=3*5 y 35=5*7
Por otro lado si trabajáramos con p=28, no primo, tenemos por ejemplo que no existe un inverso para 12, pues
mcd(12,28)=4, dado que 12=4*3 y 28=4*7.
Al trabajar con p siendo primo, todo número de nuestro conjunto tendrá un inverso y podremos calcular los inversos necesarios para calcular las pendientes:
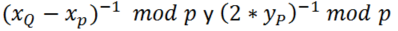
Para determinar los inversos modulo p se puede utilizar el Algoritmo Extendido de Euclides el cual no detallamos acá para no extendernos demasiado.
Con esto ya podemos calcular nuestra clave pública a partir de la clave privada!!
En el siguiente link dejamos un código en Haskell que calcula claves públicas a partir de clave privadas!
Por simplicidad se representan los números en hexadecimales.
Comprobemos con nuestro código el siguiente ejemplo del libro Mastering Bitcoin donde nos dan la clave pública asociada a una clave privada.

La función emult k x calcula k*x donde k es la clave privada, y x es nuestro punto generador.
Llamamos entonces a: emult k g, donde
k=1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD
Y G es el punto generador que definimos anteriormente.
Resultado:

Los valores de k y g (=G) están definidos dentro del script.
Lo logramos, determinamos la clave pública!!
¿Cuantas claves distintas hay?
Al trabajar con la operación modulo obtenemos que existe una cantidad finita de puntos (x,y) que pertenecen a la curva E modulo p.
Resulta que si empezamos a sumar G a si mismo varias veces, llega un punto, valga la redundancia, en el que el resultado vuelve a ser G y empezamos de nuevo el ciclo G, 2G, 3G, etc.
A este número de veces lo llamamos n, y decimos que n es el orden de G para la curva E.
Esta es la razón por la que las claves privadas, kpr, deben ser un número entre 1 y n-1, de lo contrario existirían más de una clave privada con la misma clave pública asociada, lo cual no es deseable.
Notar que este n es el mismo n de n-1 que nombramos anteriormente cuando hablábamos de la cantidad de claves privadas posibles.
Representación de claves públicas:
Es posible que la clave pública que calculamos no se parezca a claves públicas que hayas visto en otro lugar donde la misma es una única serie de números y letras y no una punto de la forma (x,y)! ¿Qué está pasando?
Las claves públicas se pueden expresar de forma no comprimida o comprimida.
La representación convencional de las claves no comprimidas se expresan agregando “04” al principio de la coordenada x, y seguidamente la coordenada y, ambas con 64 dígitos hexadecimales. Es decir nuestra clave no comprimida seria:
04F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
En gris el prefijo, en amarillo la coordenada x, y en verde la coordenada y.
Compresión
En general se trabaja con claves públicas comprimidas, esto es con longitud reducida.
Una forma de comprimir la clave pública es simplemente indicar el valor de la coordenada x ya que la coordenada y se puede calcular directamente con la ecuación de la curva secp256k1.
Observar que para cada valor de x hay dos soluciones, ya que y puede ser par o impar. Para poder identificar la coordenada y correspondiente se agrega delante de la clave publica un 02 si el valor de y es par y un 03 si es impar.
Así, nuestra clave comprimida sería:
03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
En amarillo la coordenada x, en gris el código para indicar si la coordenada y asociada es la par o impar, en este caso es impar.
Notar como al comprimir bajamos casi al 50% el largo de la clave, reduciendo la cantidad de datos haciendo el procesamiento y el respaldo rápido y eficiente.
¿Se puede invertir el proceso?
Ahora que sabemos todas las fórmulas matemáticas para determinar la clave pública a partir de la clase privada, no podemos hacer el camino inverso? ¿No podemos dividir la calve pública entre el punto G y obtener la clave privada?
Evidentemente esto no es posible.
No existe un procedimiento inverso para hacer esta “división”. Determinar una clave privada a partir de una clave pública implica ir probando valores de kpr y multiplicarlo por G hasta que encontremos el resultado de kpu que buscamos.
La cantidad posible de claves privadas, kpr, es tan grande que aun poniendo a trabajar a todas la supercomputadoras del mundo moriríamos muchisimos años antes de poder encontrar la clave.
A este “problema” de encontrar una kpr tal que kpr*G=kpu se le llama problema del logaritmo discreteo en curvas elípticas y es el punto fundamental que explica la seguridad del sistema clave privada y clave pública.
¿Pero esto no es el mismo trabajo que hacemos para calcular la kpu?
Es decir, si elegimos una kpr grande vamos a precisar muchísimos pasos, tendremos que calcular G, 2G, 3G,…. hasta llegar a Kpr*G obteniendo así las primeras kpr claves privadas y correspondientes claves públicas.
Evidentemente esto no puede ser así ya sería el mismo trabajo que resolver el logaritmo discreto. La razón es que cuando calculamos kpr*G utilizamos un truco matemático que no se puede usar a la inversa.
Cómo calcular kpr*G de forma eficiente
Supongamos que queremos calcular ~2256*G, es decir el mayor kpr posible. Empezamos con G y lo duplicamos para obtener 2G y así seguimos, ¿Cuántos pasos precisamos?
256 obviamente! Es decir que en 256 pasos superamos aún la mayor kpr posible!
El procedimiento inverso implica calcular 1.5*1077 pasos sumando de a un G: G, 2G, 3G, 4G… etc. hasta que justo para algún valor de n encontremos que n*G se igual a la kpu que tenemos, en cuyo caso n=kpr.
Probemos otro ejemplo, esta vez un número impar, calculemos 11G en la menor cantidad de pasos posibles:
- Empezamos con G (este no cuenta como un paso ya que no realizamos ninguna operación)
- Hacemos G+G=2G
- Duplicamos: 2G+2G = 4G
- Sumamos G: G+4G = 5G
- Duplicamos: 5G+5G=10G
- Sumamos G+10G = 11G
Lo logramos hacer en 5 operaciones nada más en vez de 11 pasos que sería sumar de a uno!!
Notar que hacemos uso de la suma entre puntos distintos y suma del mismo punto, no es casualidad que hayamos visto ambos casos anteriormente!
Este método se llama duplicar y sumar basado en la representación binaria de kpr.
Los números binarios son una forma de representar los números enteros. Como el nombre implica, tenemos dos alternativas, 0 y 1. Con estos dos números podemos representar cualquier numero entero!
¿Cómo se representan los números binarios?
Primero veamos los números decimales, es decir en base 10. Cuando escribimos 1245 por ejemplo estamos diciendo que tenemos 1 vez 1000, más 2 veces 100, más 4 veces 10, más 5.
Es decir 1245 = 1*1000 + 2*100 + 4*10 +5*1 = 1*10³+2*10²+4*101+5*100
De esta forma si contamos las posiciones de los números que forman 1245 de derecha a izquierda decimos que el 5 está en la posición 0, el 4 en la 1, el 2 en la 2 y el 1 en la posición 3. Notar que la posición coincide con el exponente de 10, la base del sistema decimal. Y los números en cada posición simplemente multiplican a 10pos..
En el sistema binario simplemente cambiamos la base a 2, es decir en vez de 10 usamos el 2. Notar que en el sistema decimal usamos los números 1 al 9 en las distintas posiciones, es decir 1 número menos que la base. De esta forma en el sistema binario usamos del 0 al 1. A cada posición, o digito, le llamamos bit, así para representar el 1245 precisamos 11 bits.
Tenemos que 1245dec=10011011101bin
= 1*210+0*29+0*28+1*27+1*26+0*25+1*24+1*23+1*22+0*21+1*20 =
= 1*210+1*27+1*26+1*24+1*23+1*22+1*20
= 1024 + 128 + 64 +16 + 8 + 4 + 1 = 1245
El método consiste en representar el número kpr en binario e ir pensando que agregamos los números de derecha a izquierda dentro de casilleros que corresponden a las posiciones en binario como se ve en el esquema siguiente.
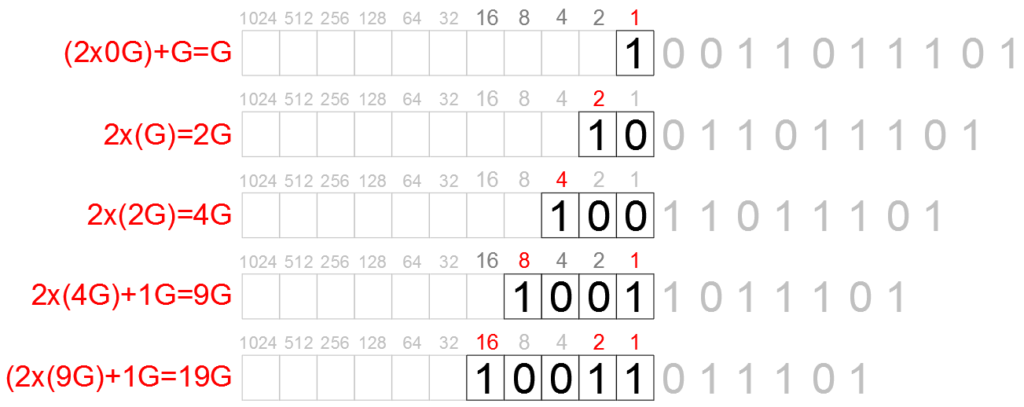
En caso de ingresar un 1 se duplica el valor anterior y se suma 1, si el número que ingresa es un 0 simplemente se duplica el valor anterior. Para el primer paso empezamos con G.
Vamos paso por paso:
1) ingresa un 1 -> empezamos con G
2) ingresa un 0 -> duplicamos el valor anterior, 2xG=2G
3) ingresa un 0 -> duplicamos el valor anterior, 2x2G=4G
4) ingresa un 1 -> duplicamos el valor anterior y sumamos 1, tenemos 2x4G+1=9G
5) ingresa un 1 -> duplicamos el valor anterior y sumamos 1, tenemos 2x9G+1=19G
Siguiendo el procedimiento se llega finalmente a 1024G!
En total precisamos 17 operaciones para calcular 1024G comparado con 1024 pasos si lo hiciéramos sumando de a un G. Esta diferencia de pasos, es decir la eficiencia, se incrementa a medida que aumenta el número total de G’s, es decir a medida que aumenta kpr.
Siendo el kpr máximo levemente inferior a 2256 tenemos que a lo sumo el numero 2256 lo podemos expresar con una serie de unos y ceros de 256 bits.
Kpr máx = n-1 =
115792089237316195423570985008687907852837564279074904382605163141518161494336
Que en binario se expresa:

Vemos que todos los bits menos 60 valen 1, es decir hay 196 unos y 60 ceros. Por lo tanto el número total de operaciones necesarias para calcular la máxima kpr posible es: 196×2+60 = 452 pasos. Esto es absolutamente despreciable frente a tener que calcular (n-1)*G sumando de a un G. Hacer estas 452 operaciones /pasos lleva un tiempo ínfimo con una computadora común y corriente!
Esta es la razón por la cual se puede calcular una kpu rápidamente a partir de una kpr!
El algoritmo más rápido conocido para realizar el camino inverso no es el de sumar sucesivamente G hasta encontrar kpu, no entraremos en detalles simplemente mencionamos que lleva del orden de 2128 pasos, suficientes para considerarlo inviable a los efectos prácticos!
Es importante notar que no hay una prueba matemática que indique que no puede resolverse de forma más eficiente, simplemente el método más rápido conocido hoy en día es demasiado lento para considerarlo una opción en la práctica.
¿Y las direcciones?
La dirección asociada a una clave pública kpu se calcula con otras funciones matemáticas que veremos en siguientes posts!
Resumen
Hemos visto en detalle que son y cómo se determinan las claves privadas y públicas para Bitcoin. Lo comprobamos con un ejemplo, proporcionamos una planilla de Excel y un código en Haskell para poder jugar con la curva elíptica y crear nuestras propias claves públicas!
Vimos como generar una clave privada no es más que elegir un número al azar y que la clave pública se determina mediante operaciones matemáticas a partir de la misma. Además mostramos como el problema del logaritmo discreto en curvas elípticas hace que determinar la clave privada teniendo la clave pública es a todos los efectos prácticos imposible!
Lo presentado en este artículo, incluido el código en Haskell, no debe usarse para crear cuentas reales de Bitcoin. El contenido es meramente educativo, se han hecho grandes simplificaciones y omisiones por practicidad y claridad. De querer implementar soluciones de uso real en Bitcoin es indispensable dominar el tema del punto de vista criptográfico, matemático y computacional.
Nos vemos la próxima con mucho más!
Bibliografía utilizada y MUY recomendada:
